Hva brukes episykliske gir til?

Episykliske girogså kjent som planetgirsystemer, er mye brukt i ulike bransjer på grunn av sin kompakte design, høye effektivitet og allsidighet.

Disse girene brukes primært i applikasjoner der plassen er begrenset, men høyt dreiemoment og hastighetsvariabilitet er avgjørende.

1. Girkasser i biler: Episykliske gir er en nøkkelkomponent i automatgirkasser, og gir sømløse girskift, høyt dreiemoment ved lave hastigheter og effektiv kraftoverføring.
2. Industrimaskiner: De brukes i tunge maskiner for sin evne til å håndtere høye belastninger, fordele dreiemoment jevnt og operere effektivt i kompakte rom.
3. Luftfart: Disse girene spiller en avgjørende rolle i flymotorer og helikopterrotorer, og sikrer pålitelighet og presis bevegelseskontroll under krevende forhold.
4. Robotikk og automatisering: Innen robotikk brukes episykliske gir for å oppnå presis bevegelseskontroll, kompakt design og høyt dreiemoment på trange steder.

Hva er de fire elementene i det episykliske girsettet?

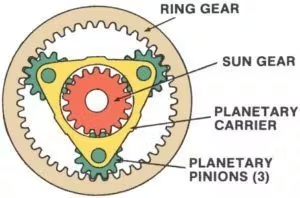
Et episyklisk girsett, også kjent som etplanetgir system, er en svært effektiv og kompakt mekanisme som ofte brukes i biltransmisjoner, robotikk og industrimaskiner. Dette systemet består av fire hovedelementer:

1. SolutstyrSolgiret, som er plassert i midten av girsettet, er den primære driveren eller mottakeren av bevegelse. Det griper direkte inn i planetgirene og fungerer ofte som systemets inngang eller utgang.

2. PlanetgirDette er flere gir som roterer rundt solgiret. De er montert på en planetgirholder og går i inngrep med både solgiret og ringgiret. Planetgirene fordeler lasten jevnt, noe som gjør systemet i stand til å håndtere høyt dreiemoment.

3.PlanetbærerDenne komponenten holder planetgirene på plass og støtter rotasjonen deres rundt solgiret. Planetbæreren kan fungere som et inngangs-, utgangs- eller stasjonært element, avhengig av systemets konfigurasjon.

4.RinggirDette er et stort ytre tannhjul som omslutter planetgirene. De indre tennene på ringgiret går i inngrep med planetgirene. I likhet med de andre elementene kan ringgiret fungere som inngang, utgang eller forbli stasjonært.

Samspillet mellom disse fire elementene gir fleksibiliteten til å oppnå forskjellige hastighetsforhold og retningsendringer innenfor en kompakt struktur.

Hvordan beregne girforholdet i et episyklisk girsett?

Girforholdet til enepisyklisk girsett avhenger av hvilke komponenter som er faste, inngang og utgang. Her er en trinnvis veiledning for å beregne girforholdet:

1. Forstå systemkonfigurasjonen:

Identifiser hvilket element (solen, planetbæreren eller ringen) som er stasjonært.

Bestem inngangs- og utgangskomponentene.

2. Bruk den grunnleggende girutvekslingsligningen: Girutvekslingen til et episyklisk girsystem kan beregnes ved hjelp av:

GR = 1 + (R / S)

Hvor:

GR = Girforhold

R = Antall tenner på ringgiret

S = Antall tenner på solhjulet

Denne ligningen gjelder når planetbæreren er utgangen, og enten solen eller ringgiret er stasjonært.

3. Juster for andre konfigurasjoner:

• Hvis solgiret står stille, påvirkes systemets utgangshastighet av forholdet mellom ringgiret og planethjulet.
• Hvis ringgiret er stasjonært, bestemmes utgangshastigheten av forholdet mellom solgiret og planetbæreren.

4. Revers girforhold for utgang til inngang: Når du beregner hastighetsreduksjon (inngang høyere enn utgang), er forholdet enkelt. For hastighetsmultiplikasjon (utgang høyere enn inngang), inverter det beregnede forholdet.

Eksempelberegning:

Anta at et girsett har:

Ringgir (R): 72 tenner

Solgir (S): 24 tenner

Hvis planetbæreren er utgangen og solgiret er stasjonært, er girforholdet:

GR = 1 + (72 / 24) GR = 1 + 3 = 4

Dette betyr at utgangshastigheten vil være fire ganger lavere enn inngangshastigheten, noe som gir et reduksjonsforhold på 4:1.

Å forstå disse prinsippene lar ingeniører designe effektive og allsidige systemer skreddersydd for spesifikke applikasjoner.